Волошина Рита Григорьевна, практический психолог;
Фирсова Наталия Николаевна, заместитель директора по учебной работе, преподаватель математики ГПОУ «Макеевский политехнический колледж»
Пожалуй, не существует ни одной науки, в которой не присутствовали бы психологические аспекты. Но особая связь у психологии просматривается с математикой. И, хотя математика никогда не претендовала на решение проблем психологии, необходимо признать, что именно она дает количественный анализ качественной определенности психологических понятий и позволяет преобразовывать данные психологических исследований в удобную конкретную для понимания форму. Математика и психология в своем взаимодействии не ограничиваются только обработкой данных, можно говорить также об анализе, обобщении, абстракции экспериментальных психологических данных для построения психологических теорий.
Психологам еще предстоит поставить много задач перед математической наукой, чтобы получить новые направления и методы, соответствующие психологической проблематике, но уже сейчас, например, широко используются предложенные С.С. Стивенсом в 1951 году шкалы наименований, порядка, интервалов и отношений (от самых слабых до самых сильных). Эти шкалы несут как психологическое, так и числовое значение. А с момента издания в 1965 году трехтомника «Руководства по математической психологии» мир имеет представление о проблеме моделирования в математике и психологии.
Безусловно, психология чаще всего имеет дело со случайными величинами. Большинство психических процессов выглядят случайными, потому что очень изменчивы, непредсказуемо вариативны и многообразны из-за сочетания многочисленных внутренних и внешних причин и обстоятельств.
Например, в психологии труда используется оценка времени реакции водителей. Время реакции человека является случайной величиной, которая характеризуется двумя параметрами: математическим ожиданием и дисперсией. Для того, чтобы установить факт влияния на время реакции, например, такого фактора, как утомление, нужно сравнить два условных распределения: до утомления водителя и после утомления (состояние человека отдохнувшего и уставшего). Само утомление – понятие психологическое, но доказать его можно, как выясняется, только математически.
Таким образом, математическая обработка психологических данных позволяет делать выводы в психологических исследованиях.
Связь этих наук, так или иначе, затрагивают почти все авторы в своих исследованиях. Ведь именно математика позволяет количественно сравнивать явления, проверять правильность словесных утверждений и тем самым добираться до истины либо приближаться к ней. Математика делает обозримыми, свойственные психологии, длинные и подчас туманные словесные описания, проясняет и экономит мысль.
Математические методы позволяют обоснованно прогнозировать будущие события, вместо того, чтобы гадать на кофейной гуще или как-либо иначе. В общем, польза от применения математики в психологии велика, но и труда на ее освоение требуется много. Однако он окупается сполна.
Психология в своем научном становлении неизбежно должна была пройти и прошла путь математизации, и сейчас это не вызывает никаких сомнений. Математический объект — это продукт человеческой мысли, материализованный хотя бы в одной из пяти основных форм: вербальной, графической, табличной, символической или аналитической. А математические методы — это правила преобразования этих объектов в доступные пониманию обывателя.
В наиболее общем виде взаимосвязи математики и психологии представлены на следующей схеме:
Обобщая вышеизложенное, можно заявить, что если в математике, например, мышление это инструмент исследования, то в психологии — и инструмент и объект, стало быть, разрывать эти две науки не имеет смысла и даже преступно.
Математическое образование — это часть общечеловеческой культуры. Любому гуманитарию необходима культура мышления, способность к интеллектуальной работе. Математика – мощнейшее средство развития культуры мышления через мобилизацию нервных процессов, ответственных за анализ и синтез, из которых, по мнению И.М.Сеченова и И. П. Павлова, и состоит мыслительная деятельность.
Для активизации творческого потенциала студентов, способных к самостоятельной интеллектуальной деятельности, необходимо от формального заучивания методов решения задач перейти к заинтересованному освоению математики. При этом следует использовать тот уникальный гуманитарный потенциал, которым обладает математика.
В образовании неслучайно в последние годы все чаще заходит речь о гуманизации и гуманитаризации математического образования.
Нужен ли обществу в принципе гуманитарий, которому не под силу разобраться в тексте учебника, рассчитанного на пятиклассника, в то время как явления, изучаемые психологией, несоизмеримо сложнее тех, которые можно формализовать и описать с помощью функции одной переменной? Возможно, лишь некоторая часть учебного материала по математике (знания, умения, навыки) непосредственно потребуется будущим специалистам в их практической деятельности, лишь ничтожный процент обучаемых в своей профессиональной деятельности будет вычислять производные, интегралы и т. д. Однако, жизненный и профессиональный успех большинства будет зависеть от степени развития их умственных способностей, культуры мышления, умения применять знания в нестандартных ситуациях, самостоятельной творческой деятельности, прекрасной гимнастикой для которых является математика в симбиозе с психологической наукой.
Несмотря на техническую направленность обучения, в нашем колледже циклу общих гуманитарных и социально-экономических дисциплин отводится значительное количество часов. Интеграция учебных дисциплин позволяет дать будущему специалисту наглядное представление о возможностях применения знаний и умений из дисциплин этого цикла к своей профессиональной деятельности.
Mеждисциплинарная интеграция знаний очень важна для современного обучения и должна рассматриваться не только с точки зрения взаимосвязей знаний по учебным дисциплинам, но и как интегрирование технологий, методов и форм обучения. От этого будет зависеть успех, а значит и результат обучения.
Предполагаем, что одной из возможностей для реализации междисциплинарных связей, которые позволяют интегрировать знания из разных областей для решения одной проблемы и позволит применить полученные знания на практике могли бы стать бинарные занятия. В рамках обучения в колледже они не носят глобальный характер, но могут представлять собой краткосрочный междисциплинарный проект преподавателей-единомышленников и студентов. Для повышения мотивации к изучению психологической дисциплины и повышения ее престижа, для доказательства необходимости изучения математики, как жизненно важной науки, бинарные занятия представляют собой важнейший инструмент. Мы нашли точки соприкосновения своих интересов в дисциплинах Математика и Психология для формирования умений и навыков, обобщения и систематизации знаний, а, главное, для доказательства невероятной неразрывной связи этих наук. Бинарные занятия требуют большой подготовки, как преподавателей, так и студентов, но их эффективность не требует доказательства.
Ярким примером теснейшей связи психологии и математики может являться такой математический объект как матрица.
Прямоугольной матрицей называется совокупность чисел, расположенных в виде прямоугольной таблицы, содержащей n строк и m столбцов,
В зависимости от количества строк и столбцов матрицы, а также от значения ее элементов различают следующие виды матриц: квадратные, диагональные, единичные, нулевые, вектор-строки, вектор-столбцы.
Для матриц определены следующие линейные операции: сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу. Определена также операция транспонирования.
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц.
Основным применением матриц было решение систем линейных уравнений. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
В психологии понимание термина сходно с данным термином в математике, но взамен математических объектов подразумеваются некие «психологические объекты», например, тесты.
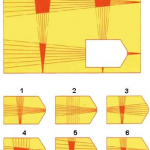
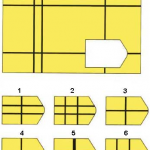
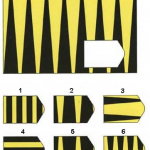
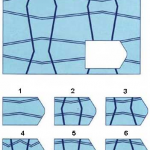
Прогрессивные матрицы Равена – тест на наглядное и в то же время абстрактное мышление по аналогии (тест интеллекта), разработанный англ. психологом Дж. Равеном (1938).
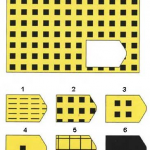
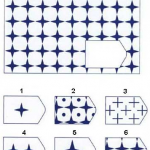
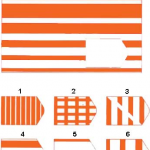
Каждая задача состоит из 2 частей: основного рисунка (какого–либо геометрического узора) с пробелом в правом нижнем углу и набора из 6 или 8 фрагментов, находящихся под основным рисунком. Из этих фрагментов требуется выбрать один, который, будучи поставленным на место пробела, точно подходил бы к рисунку в целом. Прогрессивные матрицы Равена разделяются на 5 серий по 12 матриц в каждой. Благодаря увеличению числа элементов матриц и усложнению принципов из взаимоотношений задачи постепенно усложняются как в пределах одной серии, так и при переходе от серии к серии. Имеется также облегченный вариант прогрессивных матриц Равена, предназначенный для исследования детей и взрослых с нарушениями психической деятельности.
На рисунке показаны примеры таких матриц:
Матрицы являются незаменимым средством описания многомерных объектов. Многомерную матрицу легко изобразить на плоскости, как в целом, так и по частям. Этим обеспечивается своеобразная «символистическая» наглядность матричных описаний в психологии.
Например, для психодиагностики социальных общностей малого объема (из нескольких человек) — так называемых «малых групп», социопсихолог Дж. Морено предложил использовать социоматрицы и социограммы, являющиеся элементами метода социометрии.
Социоматрица — это квадратная помеченная матрица, в строках и столбцах которой обозначены члены группы, а элементами матрицы являются условно обозначенные отношения влечения либо отвращения. По преобладанию определенных элементов в матрице можно количественно определить степень эмоциональной связности, разобщенности или даже враждебности между членами одной или нескольких групп, выделить лидеров и отверженных, друзей и врагов, недругов.

Таким образом, по нашему мнению, для решения вышеупомянутых проблем усиления мотивации к изучению психологической дисциплины и повышения ее престижа, для доказательства необходимости изучения математики, как жизненно важной науки, вполне допустимо сочетание таких дисциплин, как Математика и Психология в одном занятии и наработанный опыт в этом направлении, пожалуй уже не выглядит как оксюморон.
Литература:
- Григорьев В.П., Дубинский Ю.А. Элементы высшей математики. – М.: Академия, 2008.
- Вентцель Е.С. Теория вероятностей. — М.: Высшая школа, 2009.
- Венгер А.Л. — Психологические рисуночные тесты: Иллюстрированное руководство.
- Н.И. Шевандрин. Социальная психология в образовании. Часть 1. Концептуальные и прикладные основы социальной психологии. Москва «ВЛАДОС» 1995.
- Онискевич Т.С. «Лекция по основам высшей математики. Экспресс курс для студентов психологов» БрГУ им. Пушкина 2010.
- http://psychologylib.ru
- http://psychologylib.ru